Everything vibrates! This is a fact of life and modal analysis is the technique used to characterize how structures behave dynamically. Modal analysis separates the complicated vibration pattern that can be measured in a physical domain using e.g. accelerometers into a set of modes of vibration. These modes are actually the “finger print” of a structure.
A mode of vibration is characterized by the following three modal parameters:
Natural Frequency, fi. This value is typically given in Hertz (Hz).
Damping Ratio, ζi. This value is typically represented as a fraction of the critical damping and therefore given in percent (%).
Mode shape, φi. The geometrical way the structure moves in this particular mode of vibration.
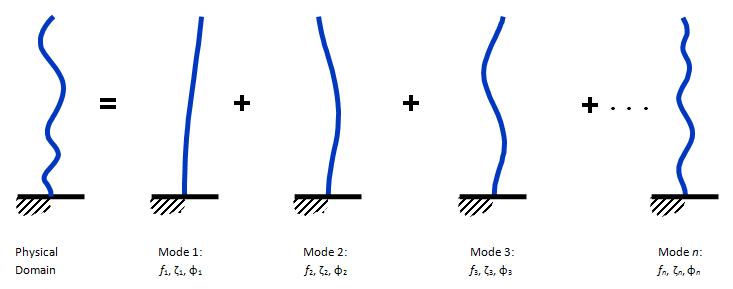
As shown in the figure above a structure typically has many modes of vibration. As the modes get higher and higher in frequency they normally also get more and more complicated modes shapes and it normally require more energy to excite these modes compared to the more simple low frequency modes.
For decades it has been possible to estimate the modes of vibration of small structures that could be taken to a laboratory and mounted in a so-called Test Rig. The Test-Rig is necessary, because the structure is not allowed to be excited by anything except some artificial excitation that can be measured.
The excitation is normally produced by either an Impact Hammer or by one or more shakers. Both these types of devices can produce a force and at the same time measure it. The figure below demonstrate how a typically setup for an Experimental Modal Analysis (EMA) is. The structure is hanging freely in a test rig, and one or more accelerometers are mounted in the positions where the response of the modes of interest is good. The impact hammer is used to impact the structure in all the positions where the modes shapes is needed. If a single accelerometer is used to measure the response the technique is normally called Single Reference technique, whereas in the case of several it is referred to as Multiple (Poly) Reference techniques.
If one or more shakers are used they will be mounted in positions where the modes of interest can be excited by them. Now it is one or more accelerometers that are moved around on the structure from measurement to measurement. Shakers are normally used for larger structures that cannot easily be excited, or if a specific input signal is desired.

Experimental Modal Analysis (EMA) – A well-proven technique for small structures
During the test there will be several sets of simultaneous measurements of the input forces and the output accelerations. These signals are transferred to the frequency domain by the so-called Fast Fourier Transform (FFT) that produces an input force spectrum and an output acceleration spectrum. The trick now is to divide the output spectrum with the input spectrum to obtain the so-called Frequency Response Function (FRF). This function shows how the structure will respond to input at a certain frequency. It is a system function that is in principle very clean, since all input is divided out of the input.
To keep the FRF clean it is very important that only the measurable force is the only excitation acting on the structure during the test. Any unmeasured input forces will cause a pollution of the FRF. The Coherence Function is normally used to evaluate the quality of the FRF.
There are cases where the Experimental Modal Analysis have difficulties in provided the expected results. It is interesting to list these as it explains why there is a need for complimentary Operational Modal Analysis tools. The limitations can be summarized in the follow list:
No external excitation during testing – Test Rig Required!
It is absolutely not allowed that any excitation that cannot be measured is exciting the structure. This will deteriorate the Frequency Response Function and therefore the modes being estimated from it.
Improper boundaries have to be accepted sometimes.
Since the structure needs to hang freely in a Test Rig the boundary conditions of it might change significantly. This will change all modal parameters obtained in this condition compared to if the structure was tested in situ.
Improper excitation levels and operating conditions have to be accepted sometimes.
Similar to the problems with the boundaries it can also be problematic with the applied excitation, since it might be very different from the excitation that the structure will experience in situ. If the structure is slightly non-linear in its behavior, then the modal parameters will change. Also if e.g. temperatures are very different in situ compared to the test especially the natural frequencies will be estimated differently.
Hammers and shakers limit applications.
Both in case of symmetric structures as well as large structures it might be difficult to excite the structures artificially in a way that is effective for the mode estimation.
In many cases it is not possible to apply the well-proven Experimental Modal Analysis. Some examples are:
Large structures, such as high rise buildings, bridges, towers and dams.
Rotating machinery, such as wind turbines, generators, engines and pumps.
Maritime structures, such as ships, submarines and offshore platforms.
In general for all these structures are that they are being subjected to some external uncontrollable in-situ forces that cause them to vibrate. Since these forces in general cannot be measured it is impossible to apply the Experimental Modal Analysis techniques that rely on the estimation of the clean Frequency Response Function.
The only thing that still can be obtained from an operating structure is the response due to the unknown excitation forces. This response is typically measured in a number of positions that is referred to as the Degrees Of Freedom (DOF). It is in these points that the modes shapes ultimately are determined.
The response is typically measured with accelerometers, but there is no reason not to use other devices that can measure dynamic response. The response can as such also be measured with laser vibrometers or strain gauges.
The major difference to Experimental Modal Analysis performed in a laboratory is that some or all of the excitation forces are unknown in case of in-situ Operational Modal Analysis.
This means that the theoretically framework in Operational Modal Analysis needs to be something different from the completely known (deterministic) input output relation – The Frequency Response Function. It is now necessary to assume something about the unknown excitation forces. When something need to be assumed the theoretically framework shifts to a stochastic framework where the input now is assumed to be a so-called stochastic process.
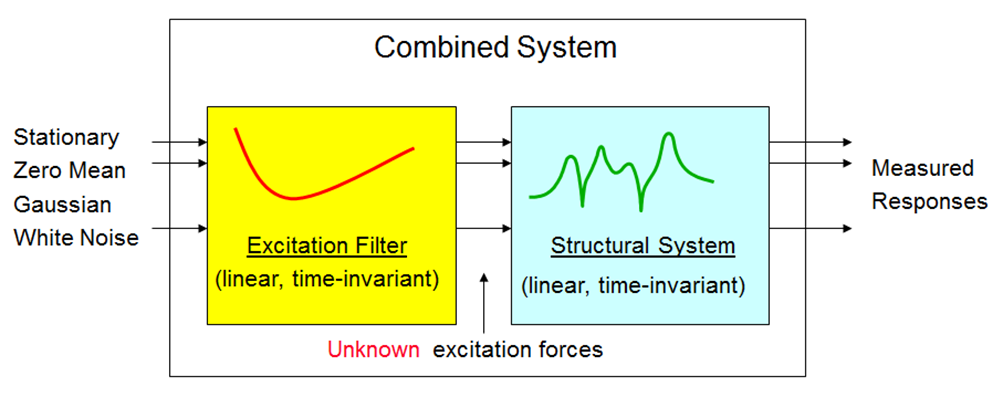
The stochastic framework used in Operational Modal Analysis
The stochastic framework used in Operational Modal Analysis assumes that the excitation that is driving the system is a so-called Gaussian White Noise Stochastic Process. This can be translated to more human language as an excitation input that has the same energy level at all frequencies we are looking at. So it means that this assumption alone imply that all modes are excited equally.
However, normally this is not the case in the real world as there is always input at some frequencies that contains more energy than others. To compensate for this, the unknown excitation forces being modeled in be this stochastic framework are assumed to be the result of a “shaping” done to the white noise. The shaping is assumed to be made by a linear filter that can shape the flat white noise into the correct shape having an energy distribution like the true unknown excitation forces.
So the response of a structure is in this framework assumed to be the output of a combined system composed by the structural system containing the dynamics of the structure being tested as well as the excitation filter that outputs the unknown excitation forces that we cannot measure.
Practical Implications
In practice the above theory imply that the excitation needed in order to perform Operational Modal Analysis must be broad-banded in the frequency range of the modes of interest. If there is nothing that persistently excites the modes during the test the result will be very poor.
It is acceptable to have very narrow-banded excitation, such as harmonic excitation, as well but there still have to be broad-banded excitation at the same time.
Another practical implication of the above framework is that some of the “modes” appearing in the measured response might not originate from the structure itself. It might actually be input “modes” that have been filtered through the structural system. In practice it means that e.g. some peaks of the spectra might not relate to the structure but to the input.
Basically there are two ways to measure in order to obtain the response needed for Operation Modal Analysis. Either all sensors are mounted once and the measurements are made, or the sensors are moved from position to position and multiple measurements are made.
When the available sensors are positioned this is referred to as being a Test Setup. A measurement made for this position of the sensors is called a Data Set. So, if the measurement is repeated for a particular Test Setup, it is simply a new Data Set. Either a single data set is used for the modal analysis or one or more of them are merged together to form longer records of data.
Single Test Setup Measurement Procedure
There are cases where it is undesirable to move around with the sensors. In these cases sensors are placed ones in a Single Test Setup. The cases where this approach is in use is e.g. in permanent monitoring systems or in cases where the measurement cannot be repeated or simply to save time.
Multiple Test Setups Measurement Procedure
In many cases though the sensors are moved around from one set of positions to another set. This is called a Multiple Test Setups measurement procedure.
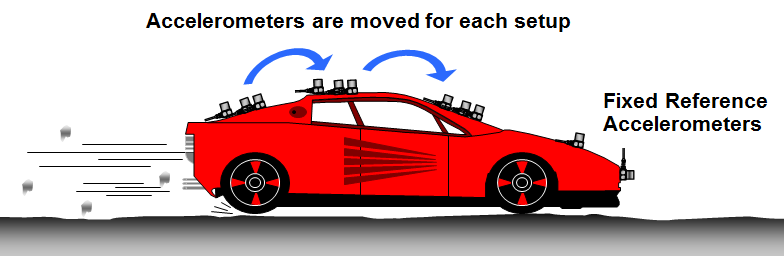
Multiple Test Setup measurement procedure
In this case a few high quality sensors are placed in positions where the modes of interest are having a good response level. These sensors are called reference sensors and are fixed in the same position when moving from one Test Setup to another. The rest of the sensors are placed in the DOF positions where mode shapes is wanted.
As the reference sensors are staying in the same positions they are basically measuring the mode shapes in these positions over and over. Since these mode shapes part should be the same from one Test Setup to the next, it provides a way to adjust the rest of the mode shape values of the different Test Setups. Normally, the adjustment is performed with some least squares fitting technique, in order to make use of the multiple references typically used.
It is extremely important that the reference sensors are positioned so that the mode shapes of the modes of interest have good amplitude in at least one of the references. Since it can be problematic to find a single position where this is the case, then recommendation is to use several references sensors in different directions and positions.
Operational Modal Analysis is not a substitute of Experimental Modal Analysis but should be considered a complimentary tool for the vast number of cases where the input foces cannot be controlled or measured.
There will still be many cases where Experimental Modal Analysis is the right tool, such as prototype testing of small structures where it is important to have same testing conditions from test to test.
However, there are just many cases where it is impossible to create such homogene conditions, especially is if structures are larger and if the excitation primarely is mother nature.